k近邻法#
kNN算法是一种基于特征向量空间的分类和回归算法,通过测量不同特征值之间的距离来进行预测。
1 分类问题1#
- 一种监督学习问题,旨在对数据分类
- 将输入数据映射到预定义的类别或标签
-
从已知的训练数据中学习一个分类模型,然后将该模型应用于新的、未知的数据,以预测其所属的类别
-
垃圾邮件过滤、金融风险评估
- 医学诊断、生物信息学
- 情感分析、客户分类
- 图像识别
2 kNN模型构建#
2.1 提出2#
- 输入:特征向量(空间点)
- 输出:类别(可以取多类)
-
已标注的训练集
-
预测:多数表决(“近朱者赤” )
- 不具有显式的学习过程
适用范围 - 数值型和标称型3
优点45 1. 直观、非参数化 2. 对异常值不敏感 3. 支持多类别
缺点6 1. 时间复杂度高 2. 存储成本高 3. “维度灾难”和数据不平衡
2.2 构建流程#
给定距离度量,k值与决策规则 [输入训练集T] 1. 在训练集 T 中找出与 x 最邻近的 k 个点,涵盖这 个点的 x 的邻域记作 \(N_k(a)\) 2. 在 \(N_k(a)\) 中根据分类决策规则决定 x 的类别 y
基本要素 1. k 值选择 2. 距离度量 3. 决策规则
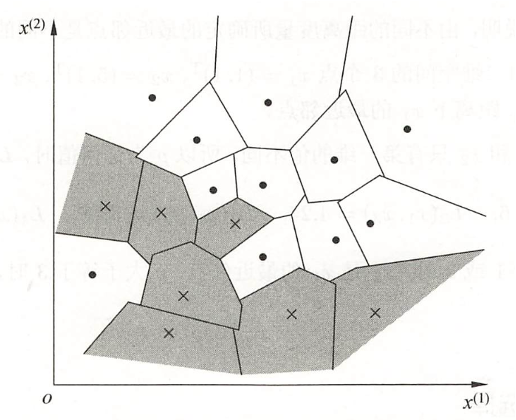
▲ 特征空间划分。
特殊情况:最近邻(k=1)
3 模型要素#
3.1 k 值选择#
| k值 | 偏小 | 偏大 |
|---|---|---|
| 近似误差 | 减小 | 增大 |
| 估计误差 | 增大 | 减小 |
交叉验证以提高泛化性能。8
3.2 距离度量9#
对于
- \(L_p\) 距离
\(\(L_p(x_i,x_j)=(\sum\limits_{l=1}^n |x_i^{(l)}-x_j^{(l)}|^p)^{1/p}\)\) - 欧氏距离
\(\(L_2(x_i,x_j)=(\sum\limits_{l=1}^n |x_i^{(l)}-x_j^{(l)}|^2)^{1/2}\)\) - 曼哈顿距离
\(\(L_1(x_i,x_j)=\sum\limits_{l=1}^n |x_i^{(l)}-x_j^{(l)}|\)\) - \(L_\infty\) 距离
3.3 决策规则#
多数表决 由输入实例的 k 个邻近的训练实例中的多数类决定输入实例的类。
- 分类函数
\(\(f:\mathbb{R}^n\rightarrow \{c_1,c_2,\cdots,c_K\}\)\) - 误分类概率
\(\(P(Y\ne f(X))=1-P(Y=f(X))\)\) - 等价于风险经验最小化
4 模型预测#
4.1 预测流程#
首先引入最简单的思路:线性扫描的方法。
▲ kNN算法流程可视化。
- 对未知类别的数据集中的每个点:
- 计算已知类别数据集众多点与当前点之间的距离;
- 按照距离递增次序排序。
- 选取与当前点距离最小的k个点:
- 选定前k个点所在类别的出现频率
- 返回前k个点出现频率最高的类别作为当前点的预测分类
- 重复步骤,完成对所有点的预测分类
4.2 Python实现#
import numpy as np
from collections import Counter
class KNN:
def __init__(self, k=3):
self.k = k
def fit(self, X, y):
self.X_train = X
self.y_train = y
def euclidean_distance(self, x1, x2):
return np.sqrt(np.sum((x1 - x2) ** 2))
def predict(self, X):
y_pred = [self._predict(x) for x in X]
return np.array(y_pred)
def _predict(self, x):
distances = [self.euclidean_distance(x, x_train) for x_train in self.X_train]
k_indices = np.argsort(distances)[:self.k]
k_nearest_labels = [self.y_train[i] for i in k_indices]
most_common = Counter(k_nearest_labels).most_common(1)
return most_common[0][0]
一个简单的例子:
X_train = np.array([[1, 2], [2, 3], [3, 4], [4, 5]])
y_train = np.array([0, 0, 1, 1])
X_test = np.array([[5, 6], [3, 2]])
clf = KNN(k=3)
clf.fit(X_train, y_train)
predictions = clf.predict(X_test)
print(predictions)
5 改进#
5.1 主要挑战#
- 前置处理:特征的选择
- 模型
- 合适的度量函数
- 合适的K值
- 降低训练和预测的复杂度
5.2 kd树#
一种二叉树数据结构,用于优化搜索算法。
优势: 1. 降低搜索维度 2. 提高搜索效率 3. 更少的存储需求 4. 支持范围搜索
可能因数据的特定分布而表现不佳。10
5.2.1 构造11#
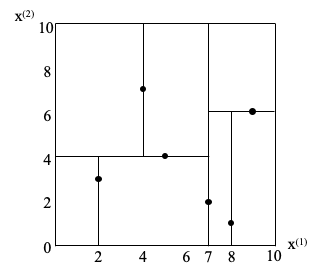
▲ kd树的构造。
- 构造根结点,使根结点对应于 k 维空间中包含所有实例点的超矩形区域。
- 递归(生成子结点):
- 选择坐标轴和切分点,确定一个超平面
- 将当前超矩形区域切分为左右两个子区域
- 直到子区域内没有实例时终止。
- 实例保存在相应的结点上。
如何选择: - 空间切分参照:坐标轴 - 切分点的选择:中位数
5.2.2 搜索#
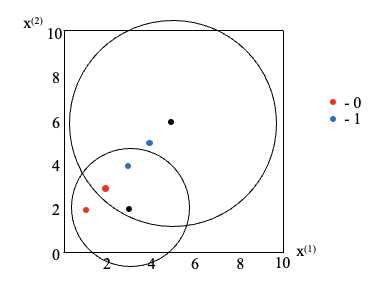
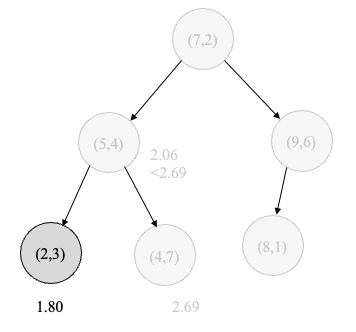
▲ kd树的搜索。
5.2.3 算法#
[输入] 已构造的 kd 树,目标点 x;
[输出] x 的 k 近邻。
- 在 kd 树中找出包含目标点 x 的叶结点:从根结点出发,递归地向下访问 kd 树。若目标点 x 当前维的坐标小于切分点的坐标,则移动到左子结点,否则移动到右子结点,直到子结点为叶结点为止。
- 构建“当前 k 近邻点集”,将该叶结点插入“当前 k 近邻点集”,并计算该结点到目标点 x 的距离。
- 递归地向上回退,在每个结点进行以下操作:
- 如果“当前 k 近邻点集”的元素数量 < k,则将该结点插入“当前 k 近邻点集”,并计算该结点到目标点 x 的距离;
- 如果“当前 k 近邻点集”的元素数量 = k,但该结点到目标点 x 的距离小于“当前 k 近邻点集”中最远 点到目标点 x 的距离,则将该结点插入“当前 k 近邻点集”,并删除原先的最远点。
- 检查另一子结点对应的区域是否与以目标点 x 为球心、以目标点 x 与“当前 k 近邻点集”中最远点的距离为半径的超球体相交。 如果相交,可能在另一个子结点对应的区域内存在距离目标点更近的点,移动到另一个子结点,接着,递归地进行 k 近邻搜索; 如果不相交,向上回退。
- 当回退到根结点时,搜索结束(若此时“当前 k 近邻点集”中的元素不足 k 个,则需要访问另一半树的结点)。
- 最后的“当前 k 近邻点集”中的 k 个点即为 x 的 k 近邻点。
5.2.4 Python实现#
class Node:
def __init__(self, data, left = None, right = None) -> None:
self.val = data
self.left = left
self.right = right
class KdTree:
def __init__(self, k) -> None:
self.k = k
def create_Tree(self, dataset, depth):
if not dataset:
return None
mid_index = len(dataset) // 2
axis = depth % self.k
sort_dataset = sorted(dataset, key=(lambda x: x[axis]))
mid_data = sort_dataset[mid_index]
cur_node = Node(mid_data)
left_data = sort_dataset[:mid_index]
right_data = sort_dataset[mid_index+1:]
cur_node.left = self.create_Tree(left_data, depth + 1)
cur_node.right = self.create_Tree(right_data, depth + 1)
return cur_node
def search(self, tree, new_data):
self.near_point = None
self.near_val = None
def dfs(node, depth):
if not node:
return
axis = depth % self.k
if new_data[axis] < node.val[axis]:
dfs(node.left, depth + 1)
else:
dfs(node.right, depth + 1)
dist = self.distance(new_data, node.val)
if not self.near_val or dist < self.near_val:
self.near_val = dist
self.near_point = node.val
if abs(new_data[axis] - node.val[axis]) <= self.near_val:
if new_data[axis] < node.val[axis]:
dfs(node.right, depth + 1)
else:
dfs(node.left, depth + 1)
dfs(tree, 0)
return self.near_point
def distance(self, point_1, point_2):
res = 0
for i in range(self.k):
res += (point_1[i]-point_2[i]) ** 2
return res ** 0.5
data_set = [[2,3],[5,4],[9,6],[4,7],[8,1],[7,2]]
new_data = [1,5]
k = len(data_set[0])
kd_tree = KdTree(k)
our_tree = kd_tree.create_Tree(data_set, 0)
predict = kd_tree.search(our_tree, new_data)
print(predict)
5.3 马氏距离#
由P.C. Mahalanobis提出;基于样本分布的一种距离测量。
- 考虑特征之间的相关性
- 对数据的缩放不敏感
- 考虑协方差结构
- 适用于异常值和噪声数据12
广泛用于分类和聚类分析。
-
垃圾邮件过滤:自动将电子邮件分为垃圾邮件和非垃圾邮件。
医学诊断:基于患者的症状数据来诊断疾病或预测病人的疾病风险。
金融风险评估:根据客户的财务和信用记录来评估客户的信用风险。
情感分析:根据文本数据中的情感内容对文本进行情感分类,如积极、消极或中性。
图像识别:对图像进行分类,例如识别数字、物体或人脸等。
生物信息学:基因序列分类,如预测蛋白质功能或基因表达模式。
客户分类:根据客户的行为和偏好将客户分成不同的市场细分。 ↩ -
KNN算法于1948年由Cover和Hart提出。
存在一个样本数据集合,也称作训练样本集,并且样本集中每个数据都存在标签,即我们知道样本集中每个数据与所属分类的对应关系。输入没有标签的新数据后,将新数据的每个特征与样本集中数据对应的特征进行比较,然后算法提取样本集中特征最相似数据(最近邻)的分类标签。一般来说,只选择样本数据集中前k个最相似的数据。k一般不大于20,最后,选择k个中出现次数最多的分类,作为新数据的分类。 ↩ -
数值型数据是指具有数量意义的数据,可以进行数学运算和比较。这种数据通常表示为数字,例如年龄、温度、身高等。在机器学习中,数值型数据常用于回归分析和连续变量的预测。标称型数据则是指无序分类的数据,其中每个值代表一个类别而没有数量意义。标称型数据通常表示为符号或字符串,例如血型、性别、品种等。在机器学习中,标称型数据通常用于分类问题,其中算法需要将输入数据映射到预定义的类别或标签。
k最近邻算法 (kNN) 适用于处理这两种类型的数据。对于数值型数据,它可以基于数值之间的距离进行分类;对于标称型数据,它可以根据邻近样本的标签进行投票,并将测试样本分类为获得最多投票的类别。因此,kNN 算法对于这两种数据类型都有较好的适用性。
还有其他类型:
顺序型数据:顺序型数据是一种具有顺序或等级关系的数据类型,其中数据值之间存在某种顺序关系,但没有明确的数值差异。例如,学历等级(如小学、初中、高中、大学等)可以被视为顺序型数据。
时间序列数据:时间序列数据是按照时间顺序排列的数据集合,通常是在一系列连续时间点上收集的数据。例如,股票价格、天气数据、经济指标等都属于时间序列数据。
区间型数据:区间型数据是指数据值表示某个范围内的值,而不是特定的数值。这种数据类型通常用于表示测量的范围。例如,温度范围、年龄段等可以被视为区间型数据。
比率型数据:比率型数据是具有固定比例关系的数据类型,其中数据之间存在明确的比率关系。比率型数据具有绝对零点,可以进行比较和数学运算。例如,长度、重量、时间间隔等都属于比率型数据。
文本数据:文本数据是指以自然语言形式表示的数据,通常包含语句、段落或文档。处理文本数据通常需要使用自然语言处理技术来提取、转换和分析文本信息。 ↩ -
老师反馈:这里的表述并不严谨,模型需要通过交叉验证来确认参数 k ↩
-
简单直观,非参数化:kNN 是一种非参数化方法,不对数据的分布做任何假设。因此,在处理复杂的数据集和未知的数据分布时,它通常具有很好的适应性。
对异常值鲁棒:kNN 对异常值比较鲁棒,因为它基于周围数据点的多数投票来确定分类,可以减少异常值对结果的影响。
适应多类别问题:kNN 能够很好地适应多类别分类问题,因为它可以通过投票的方式来确定一个实例所属的类别。
但是对高维数据的处理效率较低,需要大量的存储空间和计算时间;在数据不平衡或噪声较多的情况下,它可能会产生较差的分类结果。 ↩ -
计算成本高:kNN 算法需要计算每个测试点与所有训练点之间的距离,因此在处理大规模数据集时,计算成本会变得非常高。
存储成本高:除了计算成本高外,kNN 算法还需要存储整个训练集,这对于大规模数据集来说会占用大量的存储空间。
维度灾难:随着数据维度的增加,kNN 算法的性能可能会下降,因为在高维空间中,数据点之间的距离变得更加稀疏,导致算法的效率降低。
数据不平衡问题:在处理数据不平衡或噪声较多的数据集时,kNN 算法可能会受到数据分布的影响,从而导致分类性能下降。 ↩ -
指标函数 \(I\): 满足条件时为1.
k 近邻法中,当训练集、距离度量(如欧氏距离)、k 值及分类决策规则(如多数表决)确定后,对于任何一个新的输入实例,它所属的类唯一地确定。这相当于根据上述要素将特征空间划分为一些子空间,确定子空间里的每个点所属的类。这一事实从最近邻算法中可以看得很清楚。
特征空间中,对每个训练实例点 2,距离该点比其他点更近的所有点组成一个区域,叫作单元(cell)。每个训练实例点拥有一个单元,所有训练实例点的单元构成对特征空间的一个划分。最近邻法将实例 ai的类 yi 作为其单元中所有点的类标记(classlabel)。这样,每个单元的实例点的类别是确定的。 ↩ -
近似误差是指模型用于近似真实关系的误差,通常表示模型与真实值之间的差异。
估计误差是指使用样本数据估计整体数据集特征时产生的误差。在 kNN 中,估计误差通常与样本的选择和样本的分布有关。
K值的减小:模型变得复杂,容易发生过拟合。相当于用较小的邻域中的训练实例进行预测,只有与输入实例较近的(相似的)训练实例才会对预测结果起作用,对噪声敏感,即预测结果会对近邻的实例点非常敏感。如果邻近的实例点恰巧是噪声,预测就会出错。换句话说,k 值的减小就意味着整体模型变得复杂,容易发生过拟合。
K值的增大:就意味着整体的模型变得简单.产生更平滑的决策边界,但可能会忽略数据的局部特征。这时与输入实例较远的(不相似的)训练实例也会对预测起作用,使预测发生错误。k 值的增大就意味着整体的模型变得简单。
k 值一般取一个比较小的数值。通常采用交叉验证法来选取最优的k 值。具体可以取部分训练集作为测试集,在不同取值条件下观察最优值。 ↩ -
特征空间中两个实例点的距离是两个实例点相似程度的反映。k 近邻模型的特征空间一般是 n 维实数向量空间 \(R^n\),使用的距离是欧氏距离,但也可以是其他距离,如更一般的 \(L_p\) 距离或 Minkowski 距离。 ↩
-
实现 k 近邻法时,主要考虑的问题是如何对训练数据进行快速 k 近邻搜索。这点在特征空间的维数大及训练数据容量大时尤其必要。k 近邻法最简单的实现方法是线性扫描。这时要计算输入实例与每一个训练实例的距离。当训练集很大时,计算非常耗时,这种方法是不可行的。为了提高k 近邻搜索的效率,可以考虑使用特殊的结构存储训练数据,以减少计算距离的次数。具体方法很多,下面介绍其中的 kd 树方法。
使用 kd 树相比直接计算方法的主要好处在于它可以有效地减少计算量。kd 树是一种二叉树数据结构,它可以用于优化搜索算法,特别是在高维空间中。
以下是 kd 树相对于直接计算方法的一些优势:
降低搜索维度:kd 树能够将搜索范围缩小到与搜索点最近的局部区域,从而避免不必要的计算。
提高搜索效率:在具有大量数据点的高维空间中,kd 树可以更快地定位最近邻居,因为它可以避免对所有数据点进行逐一比较。
更少的存储需求:相对于直接计算方法,kd 树通常需要更少的存储空间,因为它可以通过二叉树结构有效地组织数据。
支持范围搜索:除了最近邻搜索之外,kd 树还可以很容易地扩展到支持范围搜索,以查找在给定半径内的所有邻居。
尽管 kd 树具有这些优势,但它可能会因数据的特定分布而表现不佳。例如,在存在大量密集聚集数据点的区域,kd 树的性能可能会下降。因此,在实际应用中,应该根据数据集的特点选择合适的算法来进行近邻搜索。 ↩ -
kd 树是一种对 k 维空间中的实例点进行存储以便对其进行快速检索的树形数据结构。kd 树是二叉树,表示对 k 维空间的一个划分。构造 kd 树相当于不断地用垂直于坐标轴的超平面将k 维空间切分,构成一系列的飞 维超矩形区域。kd树的每个结点对应于一个k 维超矩形区域。
构造 kd 树的方法如下:构造根结点,使根结点对应于 k 维空间中包含所有实例点的超矩形区域:通过下面的递归方法,不断地对 k 维空间进行切分,生成子结点。在超矩形区域(结点)上选择一个坐标轴和在此坐标轴上的一个切分点,确定一个超平面,这个超平面通过选定的切分点并垂直于选定的坐标轴,将当前超矩形区域切分为左右两个子区域(子结点);这时,实例被分到两个子区域。这个过程直到子区域内没有实例时终止(终止时的结点为叶结点)。在此过程中,将实例保存在相应的结点上。
平衡树:使用中位数作为划分点可以保证树的相对平衡,避免出现极端情况下的不平衡树结构,从而使得搜索效率总体比较高,但未必最优。考虑一些离群点。 ↩ -
考虑特征之间的相关性:马氏距离能够考虑数据特征之间的相关性,而欧氏距离只考虑各个维度之间的直线距离。这意味着马氏距离在具有相关特征的数据集上能够提供更加准确的距离度量。
对数据的缩放不敏感:在某些情况下,数据的不同特征可能具有不同的度量单位或尺度。马氏距离能够对数据的缩放不敏感,因此可以更好地处理这种情况,而欧氏距离可能受到数据尺度的影响。
考虑协方差结构:马氏距离考虑了数据的协方差结构,因此可以更好地捕捉数据特征之间的线性关系。这使得马氏距离在处理多元正态分布数据时能够提供更加准确的距离度量。
适用于异常值和噪声数据:马氏距离能够对异常值和噪声数据具有更好的鲁棒性,因为它考虑了数据的协方差结构,可以减少这些异常值对距离度量的影响。 ↩